狀態方程的開發經歷了由最初的經驗表達到具有一定理論基礎的發展過程。理想氣體狀態方程是形式最簡單的狀態方程，但它不適用于真實氣體。范德華方程是第一個適用于真實流體的狀態方程，也是最早可用于氣液兩相計算的狀態方程，其表達式為：z=V/(V-b)-a/(RTV)，這里的參數a、b分別反映了分子之間的吸引和排斥作用，它在一定程度上體現了真實流體分子間的相互作用，且三次多項式的特點也使得氣液平衡的計算成為可能，它可定性的描述出高壓下5種不同類型的相圖。雖然范德華方程的計算精度并不高，但后來工業上廣泛應用的立方型狀態方程都是在范德華方程的基礎上對引力項進行修正和改進得到的，例如，Redlich-Kwong (RK) 方程、Soave-Redlich-Kwong (SRK) 方程、Peng-Robinson (PR) 方程、Patel-Teja (PT) 方程等等。

1873年，范德華提出了最早可用于氣液兩相計算的狀態方程，其表達式為：

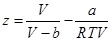                                         (1)

式中，z為壓縮因子(z = pV/RT)，T為溫度，V是體積，p是壓力，R是氣體普適性常數。參數a是分子間吸引力的度量，參數b是由于分子間斥力對分子體積的修正(如果分子為直徑σ的硬球，則b=2πNσ³/3)，參數a、b可以由流體的臨界性質計算得到。根據分子間排斥力和吸引力對狀態方程貢獻的不同，范德華方程也可以看作由硬球項(排斥項) + 吸引項所組成的方程。范德華方程只能對氣、液相以及兩相的相互轉換進行定性的描述。對臨界性質的計算以及對汽液平衡的計算誤差則較大。如由范德華方程預測不同流體的臨界壓縮因子的值均為0.375，而實際流體的臨界壓縮因子在0.24到0.29之間。隨后，范德華方程被許多計算精度更高的方程所取代，這些方程通常在范德華方程的基礎上對其斥力項和/或引力項進行修正和改進得到的。

1949年，Redlich和Kwon對范德華方程的引力項進行了修改，提出了RK狀態方程：

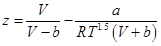                                (2)

對純物質，RK方程參數a、b的表達式為：

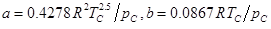              (3)

式中，R為氣體普適性常數，T_C、p_C分別代表臨界溫度和臨界壓力。Carnahan和Starling用RK狀態方程計算了各種純物質的氣相生成焓，其中包括一些極性以及/或者非對稱物質，結果顯示RK方程的計算精度較范德華方程有顯著的提高。Abbott用RK方程計算了簡單純流體如Ar、Kr和Xe (它們的偏心因子都等于零)，得到較好的計算結果，但是對于偏心因子不等于零的復雜純流體的計算結果并不理想。當結合一定的混合規則，RK狀態方程就可以用于混合體系的計算了。Joffe和Zudkevitch用RK方程預測二元混合物的臨界性質時發現計算結果可以通過調節參數a的值而得到大幅度的提升，Spear等人證實了RK方程可以計算二元混合物臨界性質。Spear等進一步計算了三元混合物的性質，結果發現用RK狀態方程計算三元混合物的精度比其構成的二元體系的計算精度稍差一點。RK狀態方程雖然也僅有兩個參數，但計算精度確比范德華方程有較大提高，尤其適用于非極性和弱極性的物質，不過對強極性的物質計算偏差仍然較大。另外，RK方程計算得到的臨界壓縮因子為0.333，比范德華方程的0.375更接近真實流體，說明RK方程在臨界點附近的計算偏差仍然較大。

1972年，Soave提出用溫度相關的a(T)來取代RK方程中的a/T^1.5，提出了SRK狀態方程，即：

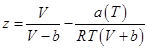                                  (4)

式(4)中

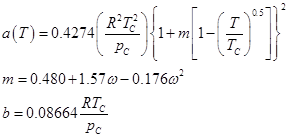          (5)

其中，ω是偏心因子。對一些烷烴化合物的蒸汽壓和含烷烴二元體系的相行為研究發現，相對于RK方程，SRK方程能更好的擬合實驗數據，而且能夠預測二元體系在臨界區的相行為。Elliott和Daubert用SRK狀態方程關聯了95種二元體系(其中包括烷烴、氫氣、氮氣、二氧化硫、一氧化碳和二氧化碳)的氣液平衡，發現SRK方程可以提高這些混合物臨界性質的計算精度，Han等也給出了對稱體系以及含甲烷體系汽液平衡的計算結果。SRK狀態方程的計算精度要比RK方程高，特別是應用于氣液平衡的計算時，所得結果較為精確，但是，SRK方程計算得到的臨界壓縮因子與RK方程同樣為0.333，并沒有改進。

1976年，Peng和Robinson將SRK狀態方程中的a(T)進行重新定義：

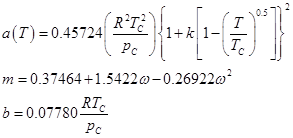      (6)

由于意識到RK和SRK狀態方程的臨界壓縮因子的值0.333仍被高估了，于是提出了一種新的體積依賴關系式：

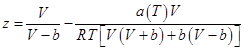                     (7)

式(7)被稱作PR狀態方程，它將RK和SRK狀態方程被高估的臨界壓縮因子進一步改進到0.307。用PR狀態方程計算純物質的飽和蒸汽壓和摩爾體積，以及二元、三元甚至多元混合物的相行為發現，PR方程可以精確地預測純物質的飽和蒸汽壓和混合物的相平衡，計算結果至少和SRK方程相當，有的優于SRK方程。Han等也報道了PR狀態方程在計算含氫氣和氮氣的混合體系的汽液平衡時更具優勢。雖然PR方程仍是兩參數狀態方程，但由于PR方程較RK方程和SRK方程改變了體積（比容）函數，因而它對體積計算的精度較RK和SRK方程都有所提高。

    1976年，Fuller提出了一個三參數的狀態方程：

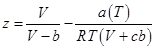                                      (8)

Fuller方程中參數c定義為協體積和體積的比例(β=b/V)，即：

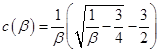                                     (9)

方程中的其他參數可由下面式子計算：

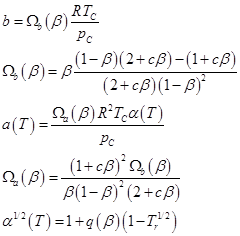
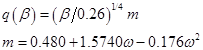                            (10)

 臨界壓縮因子的表達式為：

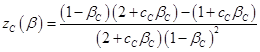                (11)

Fuller方程的修正包括兩個特點：1）對于不同物質可得到可變的臨界壓縮因子，而不會像兩參數方程那樣，臨界壓縮因子的值為一定值；2）一個新的普遍化溫度函數的產生使得方程中的參數a和b都變成了溫度的函數。實際上，Fuller方程可以退化為SRK方程或者范德華方程。當β_C=0.259921，c=1，Ω_a=0.4274802，Ω_b=0.0866404，z_C=0.333，方程即退化為SRK狀態方程；若β_C取1/3，c=0，Ω_a=0.421875，Ω_b=0.125，z_C=0.375，Fuller方程退化為范德華方程。Fuller狀態方程關聯飽和液體體積的均方根偏差在5%以內，且其對蒸汽壓的計算精度也較SRK狀態方程有所提高，計算結果顯示Fuller方程甚至能夠在合理的準確度下描述極性分子的相行為。

上述方程都是對范德華方程的引力項進行修正得到的，它們共同的特點是都可以展開成體積的三次方程，因此這類方程被統稱為立方型狀態方程。表1列出了其他一些對范德華方程引力項進行修正所得到的立方型狀態方程和它們所對應的引力項表達式。立方型狀態方程的求解可以使用解析法，但是工程上一般使用迭代法，這類方程計算耗時少，還可以進行手算，因此被廣泛應用。對于三參數或者更多參數的立方型方程而言，最大的缺陷是額外參數的確立需要額外的純物質數據。如將方程擴展到混合體系時，也至少要增加一個甚至更多的混合規則，且表達式也相對復雜，這不利于工業應用；而兩參數的立方形狀態方程，如SRK和PR方程，它們的表達形式簡單，在工業應用時，僅需要知道物質的臨界性質和偏心因子就可以方便的計算得到方程參數a、b，計算用時短且計算精度也滿足工業需求，因此，SRK方程和PR方程在工業上應用最為廣泛。

除了對范德華方程的引力項進行修正外，還有對范德華方程斥力項的改進（如表2所示）以及對引力項和斥力項同時進行修正。

 表1 對范德華方程引力項的改進

表2 對范德華方程斥力項的改進